考虑误差影响的双压力角渐开线钟表齿轮的研究

    引言

    齿轮是机械钟表中不可缺少的重要组成部分,其性能直接决定了钟表计时准确性。钟表齿轮传动突出的特点是传动比大,而从动轮(轮轴)的齿数少(6-20),这种情况决定了传动钟表中的齿轮传动一般采用钟表圆弧齿轮传动[1],采用钟表圆弧齿轮可以加工很少齿数(如6齿)的齿轮而无根切现象,这一特点满足了钟表机构中传动轮系要在比较小的空间内实现较大的传动比[2]。但是这种齿形的刀具是按照齿形制造的,刃口的成形较为困难,而且不同齿数的齿轮需要用不同的滚刀加工[3]。这使得刀具的规格大为增加,不利于生产和标准化,也使得钟表齿轮加工成本高。同时,考虑各种允许的加工误差,其力矩传动比变动率可达20%以上,即使对其齿形参数进行优化,其力矩比变动率有的也仍达20%。若用渐开线齿轮代替钟表圆弧齿轮,虽然在刀具的制造工艺上得到某些简化,但力矩比变动率仍未得到改善[4]。而且渐开线齿轮其传动效率、最小齿数等指标欠佳,不适用于速比较大的增速传动。

    钟表工业需要一种新的满足大规模制造、成本降低、性能优越的钟表齿轮齿形。为此,本文提出了一种新型钟表齿轮齿形———双压力角渐开线齿形,并对其存在制造及装配误差下的性能进行分析。

    1　考虑误差的确定

    由于误差不可避免,并且仪表机构中的齿轮模数较小,其相对误差较大,因而误差对传动性能的影响也就较大。齿轮误差有许多项,就一个齿轮来说,有齿顶圆误差、齿根圆误差、周节距误差、齿厚误差、端面跳动和径向跳动等等。对一对相啮合的齿轮来说,还有中心距误差。

    通常情况下,上述各种误差对进啮角和传动性能的影响是不相同的。其中周节距误差Δt1和Δt2、中心距误差Δa对力矩比变动率的影响较大,在设计时主要考虑上述三项。

    2　评价目标函数的确立

    为了对设计进行定量评价,必须构造包含设计变量的评价函数,称为目标函数,以F(X)表示。钟表齿轮传动性能主要是指传递效率和传递力矩。就传动性能的要求而言,由于使用目的不同而各有侧重。例如电子手表中的传动轮系希望有较高的传递效率ηj;机械式钟表中的传动轮系主要希望有较好的传动力矩平稳性,衡量的指标为力矩比变动率δij。当按传递效率ηj最大进行齿形优化设计时,得到的力矩比变动率δij当然不是最佳的;反之也然。本文针对的是机械式定时器的钟表齿轮,兼顾具有较高的传动效率,以力矩比变动率δij作为评价的目标函数较为合适。

    力矩比变动率为

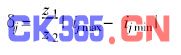
    3　约束函数的确定

    约束条件主要存在于两个方面:性能约束和几何约束。性能约束主要是预测可能被破坏或失效的特征,双压力角渐开线钟表齿轮强度方面的约束很弱,因为传动的力矩较小,主要是传动运动;几何约束主要是预测结构在静态和动态情况下各种几何上的限制因素。

    (1)小齿轮的齿顶不能变尖变尖的齿顶容易产生过早的齿顶磨损[5],全齿高变短会引起重合度下降,当此值小于1时,传动将产生周期性的冲击,因此要求

    re2

    式中  

    (2)小齿轮的齿根强度必须足够

    该约束要求小齿轮的齿根危险界面的齿厚不能太小。本文中要求其大于同模数、同齿数的仪表圆弧齿轮的齿根危险截面齿厚,由此可确定小齿轮的最小变位系数,此约束保证了齿根圆半径不至于过小。实际应用中的钟表机构中使用的小齿轮都能够满足这个条件,这是为了保证约束完整性而定义的弱约束条件。

    (3)轮齿不干涉

    若要使齿轮副在小齿轮齿根处不发生干涉,则要 

    式中,α′为啮合角。

    同理,在大齿轮齿根处不发生干涉的条件为 

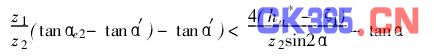
    由此条件,也可保证两齿轮齿根处的顶隙不小于(hf*-ha*)m。

    (4)非工作齿面之间的侧隙不能太小在无侧隙安装时,无侧隙中心距为a′=acosαcosα′,α′为无侧隙啮合角。那么,中心距变量Δa=a-a′=a(1-acosαcosα′),则齿侧间隙Se为

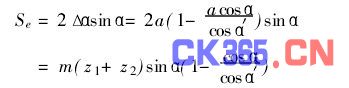
    对于模数m为0.1~1的钟表齿轮,由于齿侧间隙的平均值必须为(0.1~0.3)m,本文中将约束定为Se≥0.1m。

    (5)重合度约束

    在理论尺寸的情况下,齿轮副应使重合度大于等于1,以防止齿轮传动时产生周期性冲击,从而破坏齿轮传动的平稳性。由于本文所讨论的齿形修正方案允许了根切,所以应该是根切点不参与啮合,故 公式4

    (6)非啮合齿之间不允许出现卡齿现象

    双压力角渐开线齿轮之所以可能产生卡齿现象,是由于在齿轮加工过程中产生的周节误差。此时的传动比大于理论传动比,当啮合点到达理论啮合点时,齿廓之间的间隙最小,只要该处不发生卡齿,这在整个啮合过程中就不会发生卡齿,故 

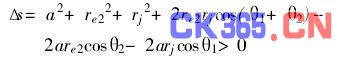
    式中,θ1=Φ1-β+invα′+γ,

    4　实例分析

    以某手表传动机构中对走时进度影响最大的条盒轮———中心齿轴为研究实例,进行具体设计,其设计条件如下:中心距a=6.93mm;主动轮齿数z1=72;从动轮齿数z2=12;主动轮转速n1=1/360r/min。

    根据目前的生产条件,取中心距误差Δa=±6.93mm,服从正态分布规律;由于两齿轮的齿距误差对进啮角的影响较大,为了满足正确啮合条件,参考现有的工艺水平,规定两齿轮的齿距误差Δt1和Δt2均为±0.004mm,服从正态分布规律。为在满足正确啮合条件的前提下,降低力矩比变动率来提高传动性能,取设计齿形的中心齿轴小齿轮的压力角为20°,条盒轮的两段渐开线齿形压力为20°和10°。

    在误差状态下双压力角齿轮的传动性能指标如表1所示,为了对照,本文也计算了目前在钟表机构中所用的圆弧齿轮的传动性能指标(相同的误差条件和误差分布规律),指标如表2所示。  表1、2

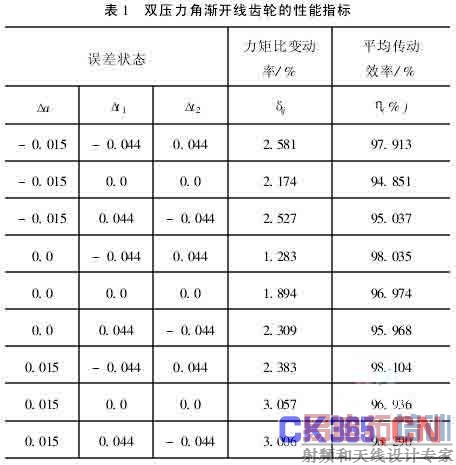
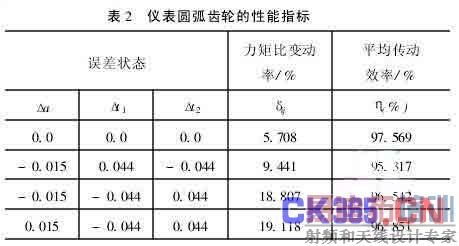
    由表1和2可以看出,两者的最大力矩比变动率分别为3.057%和19.118%,也就是说本文提出的双压力角渐开线齿轮,其力矩比变动率仅为相同条件下仪表圆弧齿轮的33.53%。

    5　结论

    通过分析,双压力角渐开线齿轮传动对制造和装配误差不敏感。双压力角渐开线齿形从理论上较好的解决了渐开线齿轮在少齿数时的根切和变位问题,在理论齿廓相啮合的情况下其力矩传动比比较平稳,效率较高,齿轮转动灵活,能满足钟表机构的工作要求。

    参考文献

    1　高恩华译.钟表机构渐开线齿轮传动的研究,钟表,1979, 7,23

    2　仙波正庄著,曹玉立译.钟表齿轮.北京:轻工业出版社,1981

    3　陈文华.计时仪器中渐开线齿轮啮合过程的分析.仪器仪表学报,1996

    4　陈文华.定力矩比齿轮传动的研究〔硕士学位论文〕.杭州:浙江大学,1987

    5　容光义.关于渐开线齿形的若干问题.山东钟表,1979(9)

    本文作者：陈晓英   陈文华

    作者简介:陈晓英(1974- ),女,浙江永康人,讲师,研究生