HFSS15: Discontinuous Galerkin Finite Element Method

The DGTD solver provides the time-domain solution of Maxwell’s Equations.

			(1)

The mathematical framework of the Discontinuous Galerkin family of numerical methods for Maxwell’s equations has been presented by Jan Hesthaven and Tim Warburton [8, 9]. To apply the DG method, we choose basis and test functions local to each mesh element T, in a similar way to the Finite Element Method:

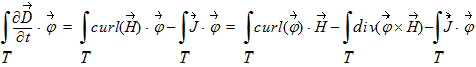
(2)

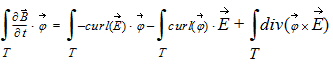
As is the case with the frequency-domain finite-element solver, the DGTD method is free of spurious solutions [10] and supports higher-order basis functions. In the time domain, the use of high orders minimizes dispersion errors occurring during the simulation of electrically large problems. The DGTD solver not only employs high-order elements but allows mixed element orders in the same mesh, known as hp-adaptivity, to optimize accuracy and solution times.

Following the same approach as in the Finite Volume Method, the divergence term containing volume integrals is transformed into surface integrals:

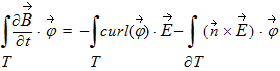
The tangential fields and are then evaluated as upwind fluxes at the surface of T by using a Riemann solver [11]. Separating the treatment inside the element from its surface provides a robust and flexible framework to take into account boundary conditions. This separation also enables various combinations of locally implicit and locally explicit time-integration schemes for instance to achieve an optimum trade-off between speed and memory, without compromising accuracy and stability.